Научные знания. Часть 1.

ГЛАВА IV

НАУЧНЫЕ ЗНАНИЯ

1

Развитие научных, или положительных, знаний достигло у древних майя значительного уровня, хотя в большинстве они были еще тесно связаны с религией. Это об­стоятельство не должно удивлять, так как известно, что во всех раннеклассовых обществах религиозная идеология являлась веду­щей и объемлющей все другие виды идеологии. О некоторых ви­дах полезных знаний мы уже писали в предыдущих главах (строи­тельная техника, металлургия для позднего периода и т. п.), оста­новимся здесь вкратце на нескольких других.

Древние майя уделяли большое внимание изучению календаря и летосчисления, математики, астрономии, медицины и истории. Кроме того, у них имелись некоторые практические сведения по географии, геодезии, метеорологии, климатологии, сейсмологии и минералогии. Однако, как уже указывалось, все эти отрасли по­ложительных знаний были тесно переплетены с религиозными учениями о демонах, божествах, знамениях и предсказаниях. Све­дения о них часто излагались весьма запутанным и перегруженным мифологическими намеками языком, и поэтому современному ис­следователю порой трудно сделать из таких текстов полезный и определенный по своей точности вывод.

В числе наиболее развитых областей науки у майя несомненно надо назвать математику или, точнее, арифметику. Еще Ланда (1955, стр. 146) отмечал способность майя легко оперировать громадными числами: «Их счет ведется по 5 до 20, по 20 до 100, по 100 до 400 и по 400 до 8000. Этим счетом они широко поль­зовались для торговли какао. У них есть другой счет, более длин­ный, который они продолжают до бесконечности, считая 8 тысяч 20 раз, что составляет 160 тысяч, затем, возвращаясь к 20, они умножают 160 тысяч на это число и так продолжают умножать на 20, пока не получат громадной цифры. Они считают на земле или на чем-либо гладком». В другом месте (там же, стр. 176), го­воря о календарном счете, Ланда пишет: «При этих возвращениях и запутанном счете удивительно видеть свободу, с которой те, кто знают [их], считают и разбираются».

В основе майяской арифметики лежала двадцатиричная система счисления, возникшая, очевидно, из осмысления и закрепления суммы числа пальцев на руках и ногах одного человека (не слу­чайно число 20 в некоторых языках майя носит название hun uinic, winak—букв, «один человек»; Kaufman, 1964, р. 114). Аналогично нашим единицам, десяткам, сотням, тысячам, миллионам и т. д. майя имели девять ступеней счета, из которых каждая после­дующая равнялась двадцати предыдущим, так что наивысшая из них составляла 25 600 000 000, если считать по десятичной системе.[103]

Большим достижением майя в области математики (очевидно, заимствованным у ольмеков и развитым ими) была разработка в период последних веков до нашей эры позиционной системы счета и математического понятия нуля (Lizardi Ramos, 1962). Оба эти понятия являются крупнейшим шагом вперед в истории мате­матического мышления. Напомним, что наша система цифровых обозначений и лежащих за ними математических понятий была разработана в Индии приблизительно в VIII в. н. э. и дости­гла Западной Европы только в XV в. Таким образом, майя ввели в употребление эти понятия задолго до того, как они по­явились у обитателей Старого Света.

Для записи чисел майя пользовались двумя системами цифр. Первая, более простая и использовавшаяся для написания любого числа, имела только три знака: стилизованное изображение ра­ковины для нуля, точки для единицы и горизонтальной черты для пяти. Отнесение той или иной цифры к разряду единиц, двадцаток (1 X 20), четырех сотен (1 X 20 X 20), восьми тысяч (1 X 20 X 20 X 20) и т. д. определялось порядковым положением данной цифры, как и в современной системе записи, но с той раз­ницей, что периоды увеличивались не справа налево, как у нас, а снизу вверх. Таким образом, число, записанное по системе майя, представляло собой вертикальный столбец. Вторая система цифр, употреблявшаяся исключительно для записи чисел, связан­ных с календарем, представляла собой четырнадцать иероглифов в виде голов божеств верхнего мира, обозначавших числа от 1 до 13 включительно и нуль. Примеры применения этих цифр в «начальных сериях» довольно многочисленны; значительно реже встречаются в надписях так называемые персонифицированные, или декоративные, иероглифы, изображающие различных мифи­ческих персонажей и животных, передающие патроны месяцев, цифры, иероглифы единиц календарного счета, дни и месяцы в циклической дате. Декоративные разновидности цифр имеют характерные признаки лицевых вариантов. Упомянем здесь такие даты на притолоке 48 из Йашчилана, стеле D в Копане, храме 26 (там же), зооморфе В в Киригуа, алтаре около зооморфа О (там же), восточной и западной стороне стелы D (там же) и на Панели рабов (здание А в Паленке).

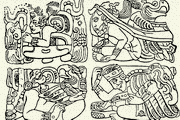
Дата персонифицрованными иероглифами 9.15.5.0.0. на стеле D. Копан.

Из надписей классического периода и трех сохранившихся рукописей мы знаем, что при своих календарных и астрономических вычислениях майя оперировали очень большими числами (большое число записано, например, на стеле 10 и в Тик'але[104] — 1 841 641 600 дней, т. е. более 5 млн лет!), но нам неизвестны ни их методы вычисления, ни пособия для таких вычислений.

Иероглифы месяцев в 365-дневном счете.
1 — Поп; 2 — Во; 3 — Сип; 4— Соц'; 5— Сек; 6 — Шуль; 7 — Йашк'ин, 8 — Моль; 9 — Ч'ен; 10 — Йаш; 11 — Сак; 12— Кех; 13—Мак; 14 — К'ан к'ин; 15 — Муан; 16 — Паш; 17 — К'айаб; 18 — Кумху; 19 — Вайеб.

А между тем подобные вычисления представляют собой серьез­ную задачу даже для современного исследователя, вооруженного целым рядом пособий и даже специальными соответствующими таблицами. Путем анализа нескольких мест из Дрезденской руко­писи и ошибок в вычислениях, имеющихся в надписях, Д. Э. С. Томпсон установил несколько интересных фактов (J. E.S. Thompson, 1941c). Во-первых, что майя при своих вычислениях не употребляли умножения или деления, а ограничивались лишь сложением и вычитанием; во-вторых, что основной единицей при календарных вычислениях у них был год в 364 дня; наконец, в-третьих, что все эти вычисления производились при помощи простого прибора типа абаки, где счетными единицами были семена какао, цветные камешки или т. п. (практически о том же говорит и Ланда в приведенном выше отрывке). Томпсон дает и несколько примеров вычислений при помощи такого прибора. Санчес (Sanchez, 1961), подробно доказав эти положения амери­канского ученого, предполагает, однако (хотя в источниках об этом нет упоминания), что майя, возможно, применяли деление и умножение. Следует попутно сказать, что Томпсон, устанавливая существование абаки, не обратил внимания на наличие в памят­никах искусства майя данных, подтверждающих его гипотезу. Так, на разбираемом нами далее (стр. 216) полихромном сосуде из Небаха мы видим позади правителя, принимающего дань, писца с таким счетным прибором в руках. Недавно, при раскопках бо­гатого захоронения в тикальском Храме гигантского ягуара, были найдены костяные палочки с вырезанными на них календарными иероглифами. Л. Саттертуэйт полагает, что они могли служить своеобразным счетным приспособлением при вычислении сложных календарных дат (Satterthwaite, 1964a).

Ни у одного из народов древней Америки мы не находим столь высоко развитых календаря и системы летосчисления, как у древних майя классического периода. Практические нужды сельского хозяйства вызвали к жизни точный календарь, который стал в руках жречества могучим орудием идеологического воз­действия на массы. Определяя наиболее удобные сроки для раз­личных земледельческих работ (отступление от них означало бы в условиях тропиков и при тогдашней системе сельского хозяй­ства подлинную катастрофу), жрецы окутывали это сложнейшей мистической символикой и сопровождали пышными религиозными церемониями. Точное летосчисление, возникшее сперва из кален­дарных потребностей, позже было связано с чисто религиозными учениями о смене богов, управляющих вселенной, и с культом правителя города-государства. Но одновременно изучение и раз­работка календаря вели к накоплению положительных знаний по астрономии, математике и метеорологии, так как жрецы должны были уметь точно вычислять периоды наступления дождей, за­сухи, появления на небе различных светил и т. д.

Научная литература по календарю майя очень велика,[105] это избавляет нас от подробного и детального его рассмотрения. Ограничимся поэтому лишь сообщением основных сведений и не­которых замечаний по отдельным вопросам.

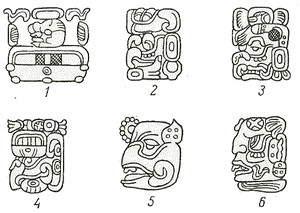
Иероглифы в «долгом счете».
1 — вводный знак; 2 — бактун, 3 — к'атун; 4 — тун; 5 — виналь; 6 — к'ин.

Календарная система майя представляет собой своеобразную и значительную главу в истории мировой науки. К сожалению, надо прямо сказать, что, несмотря на очень большое количество работ, посвященных ей, эта область еще очень далека от полного понимания. Недоумения, споры из-за того или иного вопроса, просто незнание встречаются чуть ли не на каждом шагу. Объяс­няется, конечно, это в первую очередь тем, что современные ис­следователи рассматривают пока только цифровой, математиче­ский скелет календаря, не сумев проникнуть в ту систему обра­зов, в которой его воспринимали сами древние майя. Отсюда и субъективизм отдельных исследователей, и споры между ними в истолковании тех или иных вопросов действия календарного механизма. Поясним это положение примером из истории другой области науки. Средневековые алхимики, например, несомненно знали реакции между водой и железом или золотом и ртутью, но выражали их в записях, а самое главное представляли в совер­шенно иных образах, чем современные химики. В действительности майяский жрец, производя сложные календарные вычисления, оперировал не с абстрактными числами и днями календаря, а с чрезвычайно сложной группой понятий, так как любое из них было связано в его мышлении с определенной группой мифологи­ческих образов. Это, конечно, не мешает допущению, что послед­ние для вычислительных целей могли оформляться в виде групп чисел. Но повторение такой числовой формы в циклических рас­четах вызывало в умах майяских жрецов и совершенно опреде­ленные заключения: то, что имело место в прошлом, должно повториться в будущем. Отсюда, между прочим, черты календар­ного фатализма в их мышлении, о котором часто писали С. Г. Морли и Д. Э. С. Томпсон, или, точнее говоря, вера в про­роческие свойства календаря.

Ярким примером несовпадения между нашим и майяским по­ниманием особенностей календаря и их образным представлением может служить вопрос о комбинации двух любых циклов. Во всех западных работах по календарю майя в качестве поясняющего образа приводится сцепление двух зубчатых колес (см., напри­мер: Morley, 1947, р. 270; J. E. S. Thompson, 1955, р. 150; М. D. Сое, 1966а, р. 55). Совершенно ясно, что майя не могли представлять себе таким образом взаимодействие двух циклов уже потому, что они не имели понятия о принципе действия зубчатого колеса. Вернее всего для них это взаимодействие осмыслялось как движение двух хороводов, вращающихся один посолонь, а дру­гой — в обратном направлении.

Во всех майяских системах календаря основной единицей яв­ляется день, безразлично определялся ли он как отрезок вре­мени или как числовой промежуток, выраженный интервалом между двумя датами. О делениях дня на какие-то части (часы, минуты) у майя мы ничего не знаем; сообщение Ланды (1955, стр. 165) о частях дня говорит только о его времени (подобно нашим утру, полдню, вечеру). Вероятно, один день начинался, а другой кончался во всех системах в одно и то же время: пред­положительно в момент солнечного восхода или заката. Наиме­нования дней и месяцев в различных календарях несколько отли­чаются друг от друга, а в надписях классического периода расшифрованы пока достаточно предположительно. Наиболее при­нятая система их обозначения по юкатанскому календарю доиспанского времени, конечно, абсолютно условна. В записи позиции или даты в определенном цикле обозначение дня или более долгого периода было фиксированием повторяющейся последовательности или цикла из чисел, названий либо комбинаций того и другого. Простейший пример — обозначение в нашем календаре: суббота, 13 июля, которое предусматривает сочетание двух циклов — не­дельного, из семи названий, и 12-месячного. Каждый «круглый» цикл покрывает период, после которого начинает повторяться снова та же самая комбинация дат.

Весь календарь майя представлял собой сложный механизм из циклов различных размеров. Основой его был период в 260 дней, состоявший из комбинации «недельного» цикла (13 дней) и «месячного» (20 дней). Дни первого обозначались цифрами от 1 до 13, а дни второго имели 20 названий. В комбинациях с другими циклами дни месяца также обозначались числами от 0 до 19 (пер­вый день месяца считался нулевым[106]). 260-дневный период имел распространение во всей Месоамерике и, очевидно, был тем зер­ном, из которого выросли все остальные календарные системы. Происхождение его неясно; некоторые исследователи (например, Л. Шульце-Йена; Schultze-Jena, 1933, Bd. I, SS. 28—33) свя­зывали его с нормальным периодом беременности, но более пра­вильно, конечно, искать его истоки в сельскохозяйственной дея­тельности древних обитателей Месоамерики, т. е. считать его простым сельскохозяйственным календарем. Ола Апенес и Хирард (Apenes, 1936; Girard, 1966, pp. 278—289) достаточно убе­дительно показали это. Самый ранний его образец, дошедший до нас, это надпись в Монте-Альбане, которую А. Касо (Caso, 1958, р. 73) относит по крайней мере к VI в. до н. э. Наиболее приня­тые термины в научной литературе для этого периода — tzolkin (ю), cholquih (к, как), tonalamatl или tonalpohualli (нах) — не мо­гут быть признаны удачными, так как связывают его с каким-то определенным народом, поэтому в дальнейшем он называется просто «священным периодом», следуя терминологии Л. Саттертуэйта (Satterthwaite, 1965).

Последовательность восемнадцати 20-дневных месяцев состав­ляла 360-дневный год, к которому в конце добавлялись 5 дней, носивших название «дней без имени» — хта kaba kin (ю); они считались несчастливыми. В сумме все это давало 365-дневный неопределенный год. Комбинация «священного периода» с годом, у которого отсутствовали вставные дни, составляет цикл кален­дарного круга из 52 неопределенных лет, или 18 980 дней. Таким образом, дата майя состояла из числа 13-дневной недели, назва­ния дня, числа месяца и названия месяца. Такой способ обозна­чения фиксировал не только определенный день в году, но и определенный день в 52-летнем цикле, так как однозначное соче­тание двух чисел и двух названий могло повториться только через 52 неопределенных года.

Датировка по календарному кругу была распространена у многих народов Месоамерики. Несовершенство такой хроноло­гии ясно: через некоторое время уже трудно определить, к ка­кому календарному кругу относится имеющаяся дата.

Кроме этих основных циклов майя использовали и ряд дру­гих, самого разнообразного характера. Среди них можно назвать 9-дневную неделю (очевидно, связанную с эннеадой богов ночи, как у нахуа), цикл в 819 дней, 17-дневную неделю богов земли, цикл планеты Венера со средней продолжительностью 583. 48 дней, лунный цикл (Кнорозов, 1963, стр. 261—262) и др. Объединяя такие циклы в одну систему с календарным кругом, можно получить значительно большие временные периоды. Так, включение 9-дневной недели образует цикл в 468 лет, а до­бавив еще обозначение дня в 7-дневном цикле, мы получим круг в 3276 лет.

Майя классического периода имели также летосчисление по эре, обычно называемое в литературе «долгим счетом». Происхо­ждение его тоже еще не совсем ясно, так как первые памятники, имеющие дату, записанную этим способом, найдены не на майяской территории (стела 2 в Чиапа-де-Корсо — 9 декабря 36 г. до н. э., стела С в Трес-Сапотесе — 31 г. до н. э.), но майя явно усо­вершенствовали эту систему. В американистике записи таких дат носят условное название — «начальная серия», так как они обычно помещались в начале надписи. В них указывалось коли­чество годов и дней, истекших от начальной даты — 4 Ахав 8 Кумху (по-видимому, конец последнего крушения мира и со­творение нового; по представлениям майя, их было несколько). Прошедшее время отмечалось количеством истекших дней (услов­ное обозначение, взятое из языка юкатанских майя, — kin), меся­цев по 20 дней ( uinal), годов по 18 месяцев (tun), периодов по 20 тунов (katun) и периодов по 20 к'атунов (циклов[107]), равняю­щихся каждый 144 000 дней, т. е. приблизительно 400 наших лет. Таким образом, любая дата, записанная по способу «дол­гого счета», имела приблизительно следующий смысл: «От на­чальной даты — 4 Ахав 8 Кумху — прошло 8 циклов, 14 к'атунов, 3 туна, 1 виналь и 12 к'ин до дня завершения (или посвящения) данного памятника (в этом случае взята дата на известной «лей­денской табличке»)». Современные исследователи, переводя цифры майя в наши и отбрасывая названия периодов (заменяя их пози­ционным положением чисел), записывают такую дату следующим образом: 8.14.3.1.12. В конце надписи часто писалась еще дата календарного круга (1 Эб, 0 йашк'ин в данном случае). Этот способ записи хронологических дат у майя, конечно, имел большие преимущества в силу своей точности.

Важно отметить, что «долгий счет» мыслился у майя также циклическим, т. е. после завершения 13 больших циклов отсчет начинался заново. Однако, очевидно, что период в 347 000 лет, в течение которого даты не могли повториться, представлял собой достаточно емкий промежуток времени для истории человечества. Упомянутые выше даты с большим количеством дней, вероятно, относятся к таким случаям. Правда, не все они исходят из 4 Ахав 8 Кумху. Так, например, надписи в Паленке, Киригуа и Кобе имеют другую начальную дату — 4 Ахав 4 Соц.

В наиболее полном виде дата надписей классического периода включает следующие части: 1) «начальную серию», состоящую из вводного иероглифа и пяти иероглифов периодов с цифрами, указывающими число дней, прошедших от начальной даты; 2) дату календарного круга, состоящую из числа 13-дневной недели, иероглифа дня 20-дневного месяца, числа и иероглифа месяца,. покровитель которого указан в вводном иероглифе «на­чальной серии»; 3) дня 9-дневной недели, указанного с помощью одного из 9 иероглифов дней и иероглифа недели; 4) лунной серии, состоящей обычно из пяти иероглифов, указывающих число лунного месяца, его порядковый номер и название, а также количество дней в месяце.

В надписях после «начальной серии» часто встречаются дру­гие числа, также указывающие количество дней и сопровождае­мые иероглифами единиц счета. Эти числа указывают количество дней, прошедших между календарным кругом «начальной серии» и следующим календарным кругом, поэтому их называют интер­вальными числами (старое название — «вторичные серии»). Иногда употреблялся сокращенный способ написания дат, без «начальной серии». В таком случае ставилась дата календарного круга и указывалось, на конец какого периода она приходится. Так, например, на стеле 2 в Копане имеется дата 12 Ахав 8 Кех 11 к'атунов, что соответствует «начальной серии» 9.11.0.0.0. Сле­довательно, в датах конца периода пишется не вся «начальная се­рия», а лишь один из иероглифов единиц счета с соответствую­щей цифрой. Такого рода даты обычно называют «датами конца периода». Они обеспечивали точность датировки в пределах около 19 000 лет.

Еще более несовершенным был способ датировки по к'атунам (двадцатилетиям). Он применялся на Юкатане перед испанским завоеванием (ср.: Ланда, 1955, стр. 191—: 193) и поэтому в науч­ной литературе носит название «юкатанской датировки». Суть его состоит в том, что к'атуны, заканчивающиеся днем Ахав с циф­ровым показателем, уменьшающимся постепенно на две единицы (т. е. 13 Ахав, 9 Ахав и т. д.), повторяются только два раза в четырехсотлетний период. Впервые такие даты появляются в городах Британского Гондураса (Караколь, алтарь 4) и Юка­тана (Шкалумк'ин, южное здание, и К'абах, здание 2С-6). Это казалось юкатанцам достаточно точным определением времени события. В действительности же, если отсутствует «начальная се­рия», то определить хронологическую последовательность к'атунов на большом отрезке времени не представляется возможным: точ­ность этого способа датировки уже лежит в пределах только 256 лет. Отсюда, между прочим, трудности в хронологии событий позднего периода истории майя.

Датировка по «долгому счету», т. е. способом «начальных се­рий», по неизвестным причинам оставляется майя в начале X в. (последние «начальные серии» вырезаны на нефритовой подвеске из Цибанче — 10.4.0.0.0., или 909 г., и стеле в Сан-Лоренсо, близ Ла-Муньека, штат Кампече, — 928 г.). Постепенные шаги к этому видны еще с 731 г., когда в памятниках «начальная серия» все чаще заменяется «датой конца периода». Введение «юкатанской датировки» еще более упростило запись, но осложнило задачу бу­дущих историков.

Попутно здесь следует коснуться весьма важного воп­роса о перечислении дат майяского летосчисления в нашу хроно­логическую систему. Если бы было известно соотношение даже только одной «начальной серии» с датами нашего календаря, то вычисление дат по хронологии майя не представляло бы никаких осложнений и определение, на какое число нашего календаря падал исходный день «начальной серии», не вызвало бы затруд­нений. Но двойная запись дат — по хронологической системе майя и по нашему летосчислению — имеется только в документах, отно­сящихся ко времени после испанского завоевания, т. е. к концу так называемого юкатанского периода майяской истории. В этот пе­риод майя, как мы видели, записывали даты исторических собы­тий посредством «краткого счисления», гораздо менее совершен­ного. Согласно этой системе, одноименные даты могут повто­ряться через 93 600 дней (т. е. около 256 лет).

Исходный момент «начальных серий» — 4 Ахав 8 Кумху — современные ученые могут установить только при помощи дат, выраженных в системе «краткого счисления». Поэтому исследова­тели расходятся во вопросу о выражении этой мифической на­чальной даты календаря майя в числах нашего календаря. Одни, как например Г. Д. Спинден, помещают ее на 13 октября 3373 г. до н. э.; другие (М. Эрнандес, Д. Э. Томпсон, С. Г. Морли) — на 7 сентября 3113 г. до н. э., т. е. приблизительно на 260 лет позже. Большинство специалистов в настоящее время придержи­вается последней системы пересчета дат, однако и она не может объяснить целого ряда спорных моментов.

В нашей работе даты приводятся по пересчету Д. Э. Томп­сона, так как при использовании другой системы получается раз­рыв между хронологией майя и датами других археологических культур Центральной Америки. Последние исследования методом радиоуглеродного анализа деревянных балок из тикальских хра­мов подтверждают, между прочим, датировку, предлагаемую си­стемой пересчета Эрнандеса—Томпсона (Satterthwaite, 1964b, 1965; Satterthwaite and Ralph, 1960).

Весьма значительными были успехи майя в астрономии, тесно связанной у них, как мы уже видели, с календарем. На основании многовековых наблюдений их астрономы вычислили продолжи­тельность солнечного года с точностью, превосходящей григорианский календарь, которым пользуемся в настоящее время мы. По их вычислениям длина этого года равнялась 365.2420 дням; по григорианскому календарю она составляет 365. 2425 дней, а по современным астрономическим данным — 365.2422 дня. Они умели рассчитывать наступление солнечных затме­ний, близко подошли к понима­нию 19-летнего метонова цикла. В 682 г. жрецы-астрономы Ко­пана ввели в употребление фор­мулу, по которой 149 лунных месяцев = 4400 дням. Вскоре эта формула была принята почти во всех городах классиче­ского периода.[108] По ней длина лунного месяца равнялась в среднем 29.53020 дням — цифра, очень близкая к данным наших астрономов (29.53059 дней). О календаре, основанном на наблюдениях над Венерой, уже говорилось выше. Здесь, мо­жет быть, следует только доба­вить, что на листах 24—29 Дрезденской рукописи изложен замечательный календарь Ве­неры, верный в общей слож­ности на 384 года.

Иероглифы астрономических понятий.
1 - небо; 2- Луна; 3- солнечное затмение; 4 - Венера; 5 - Земля; 6 - Марс; 7 - Солнце; 8 - Сатурн.

Майя были известны и дру­гие планеты: Марс, Сатурн, Меркурий, Юпитер. Однако здесь, как и в других астроно­мических вопросах, мнения ис­следователей так сильно отли­чаются друг от друга, что стано­вится ясным только одно: ра­бота лишь начата. Укажем, например, что листы 49—52 Дрез­денской рукописи Р. Вильсон считает относящимися к Сатурну, Крейхгауэр — к Меркурию, М. Мэйкемсон — к Марсу, Людендорф — к Юпитеру, а Д. Э. С. Томпсон вообще не видит в них никаких астрономических данных.[109]

В письменных источниках послеиспанского периода упоми­наются созвездия Плеяды, Скорпион, Малая Медведица, Близ­нецы (izab, zinaan, chimal ek, ас— ю), Млечный Путь (tam acaz, ah poou — ю), Полярная звезда (хатап ек — ю). Кратко об этом сообщает и Ланда: «Они руководствовались ночью, чтобы узнать время, Венерой, Плеядами и Близнецами» (1955, стр. 165).

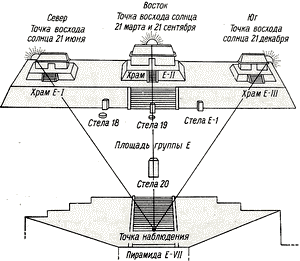
Схема астрономического комплекса. Вашактун, группа Е.

Спинден предполагает, что майя был известен зодиак, состоящий, однако, не из двенадцати, а из тринадцати домов (Spinden, 1916b). На листах 23 и 24 Парижской рукописи, по его мнению, изобра­жены знаки зодиака. А в таком случае первыми домами его должны были быть: Скорпион, Черепаха и Гремучая Змея.

Астрономические наблюдения производились майя с вершин их пирамидальных храмов невооруженным глазом; единственным ин­струментом, возможно, служили две перекрещенные палки, чтобы фиксировать точку наблюдения. По крайней мере подобные орудия изображены в рукописях Наттол, Сельдена и Бодли около жрецов, наблюдающих звезды. Кроме того, имелись специальные архитектурные комплексы, предназначенные для определения пере­ломных точек времен года. Наиболее известный из них — комп­лекс E-VII, I, II, III в Вашактуне. Его выстроили следующим образом. На западной стороне была воздвигнута пирамида E-VII, фронт которой был обращен строго на восток. Напротив нее, на восточной стороне той же площади, находилась большая вытянутая платформа с тремя храмами (E-I, Е-П, E-III) на ее верхней пло­щадке. Храмы эти были построены с таким расчетом, чтобы для наблюдателя, стоявшего на вершине пирамиды E-VII, прямо на­против стелы 20, укрепленной внизу около лестницы, солнце в день летнего солнцестояния (21 июня) появилось бы у левого (северного) угла храма E-I, а в день зимнего солнцестояния (21 декабря)—у правого (южного) угла храма E-III. В дни ве­сеннего и осеннего равноденствий солнце всходило для наблюда­теля прямо над центром крыши среднего храма Е-II.

Подобные сооружения были открыты и в других городах майя классического периода (Нак'ум Йашха, Наачтун, Балак'баль, Ушуль, Бенке-Вьехо, Калак'муль, Ишк'ун, Кахаль-Пичик, Хацкаб-Кеель, Ошпемуль, Рио-Бек II, Тик'аль, Шультун, Уканаль, Сан-Хосе, Ла-Муньека, Вашакканаль), после того как при раскопках Вашактуна был выяснен принцип их положения (Ruppert, 1940). Имелись и более простые комплексы, как например ансамбль из стел 10 и 12 в Копане, указывающий на место захода солнца 12 апреля — время начала посева (Morley, 1947, pp. 144—145).

В более позднее время появляются специальные здания, слу­жившие для астрономических наблюдений. Таким была в Чич'ен-Ице круглая башня Караколь (от исп. caracol — «улитка»), на­званная так за извивающуюся подобно раковине улитки лест­ницу, ведущую в небольшую комнату на вершине. Эта башня, помещенная на двух находящихся друг на друге прямоугольных террасах, достигает 13 м в высоту. Небольшие прямоугольные окна, прорезанные в толще ее стен, направлены на важные астро­номические пункты — точки захода солнца в день весеннего рав­ноденствия, захода луны в эту ночь и т. п. (Ruppert, 1935).

[103] Назовем основные работы по майяской математике (помимо календаря): J. E. S. Thompson, 1941c; Fulton, 1947; Long, 1948; Sanchez, 1961; Calderon, 1966.

[104] Morley, 1937-1938, v. I, pp. 308-326. Имеются и другие надписи (стела I в Кобе, стела N в Копане, камень из Чиапы и западная панель таб-летты Храма надписей в Паленке), в которых даны большие календарные числа. Дата на стеле F в Киригуа 1 Ахав 13 Йашк'ин указывает на время 91683 930 лет тому назад, а на стеле D из того же городища — около 400 млн лет (J. E. S. Thompson, 1960, pp. 314—316). Безусловно, они заслу­живают специального исследования, так как счет в них ведется от гораздо более ранней даты, чем начальная — 4 Ахав 8 Кумху.

[105] Назовем лишь основные: Morley, 1915, 1916, 1920, 1937—1938; J. E. S. Thompson, 1927, 1932с, 1937а, 1960; Spinden, 1924; Teeple, 1925a, 1925b, 1926, 1928; Satterthwaite, 1947, 1948, 1951, 1958b, 1961b, 1965; Кнорозов, 1963, стр. 30—33, 249—262; Leon-Portilla, 1968.

[106] Ряд исследователей (см., например: Satterthwaite, 1947, pp. 31—35) по­лагает, опираясь на такую нумерацию, что майя считали только истекшие единицы времени, т. е. так, как мы считаем часы.

[107] Употребляющееся в зарубежной литературе для обозначения этого пе­риода времени слово «бактун» является искусственным образованием и не засвидетельствовано в источниках, поэтому лучше избегать его применения.

[108] Л. Саттертуэйт (Satterthwaite, 1958b), основываясь на новых эпиграфи­ческих материалах из Тик'аля, приходит к выводу, что эта формула была разработана .впервые в Тик'але приблизительно на два века раньше, чем в Копане. Однако у нас нет еще промежуточных данных, которые позво­лили бы связать это тикальское новшество с распространением единой лун­ной формулы в других городах.

[109] Из многочисленной литературы по астрономии майя обращаем внимание читателя на следующие работы: Satterthwaite, 1948, 1951, 1965; J. E. S. Thomp­son, 1960; Spinden, 1916b, 1928; Teeple, 1925a, 1925b, 1926, 19.28, 1931; Willson, 1924; Smiley, 1964